KNN应用于异常检测

1. KNN

KNN最近邻分类器可以被称为一种消极学习模型（lazy learner），其并未将模型训练及测试分为两个显著的阶段，而是在需要对样本进行分类测试时在对训练样本建模，而像决策树、Logistic Regression、SVM等基于规则的分类器则可以被认为是积极学习模型（eager learner)。

算法的通俗解释

对于给定训练集，以及测试样本，在训练集中找到与该样本最近邻的K个样本点，这K个样本点的多数属于某一类，则该测试样本就可以被划分为此类别中。

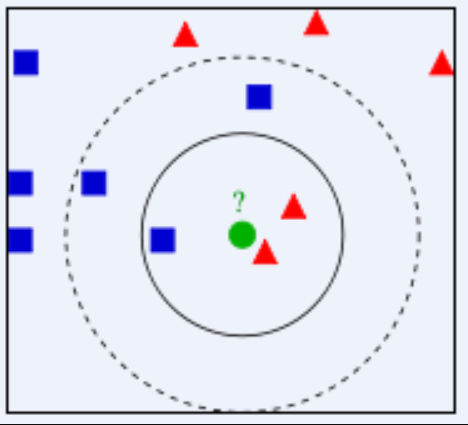
举个例子，上图包含两类样本，蓝色方形为一类，红色三角形为一类，中间绿色圆形样本为待分类的数据。

若 k = 3，绿色圆点的最近的3个邻居是2个红色三角形和1个蓝色正方形，2 > 1，所以绿色测试样本属于红色三角形这一类。
若 k = 5，绿色圆点的最近的5个邻居是2个红色三角形和3个蓝色正方形，3 > 2，所以绿色测试样本属于蓝色正方形这一类。

时间空间复杂度

KNN 分类器不需要使用训练集进行额外的训练，训练时间复杂度为0，但在测试时KNN 分类的计算复杂度和训练集中的数目成正比，也就是说，如果训练集中样本总数为 n，那么 KNN 的分类时间复杂度为至少为O(n)。

KNN算法需要大量的空间存储训练样本，适用于小样本集。

K值选择影响

K太小，最近邻分类器容易受到训练数据的噪声而产生的过拟合的影响；
K太大，最近分类器可能会误会分类测试样例，因为最近邻列表中可能包含远离其近邻的数据点。

python code

from numpy import *
import operator

class KNN:
    def createDataset(self):
        group = array([[1.0,1.1],[1.0,1.0],[0,0],[0,0.1]])
        labels = ['A','A','B','B']
        return group,labels

    def KnnClassify(self,testX,trainX,labels,K):
        [N,M]=trainX.shape
    
    #calculate the distance between testX and other training samples
        difference = tile(testX,(N,1)) - trainX # tile for array and repeat for matrix in Python, == repmat in Matlab
        difference = difference ** 2 # take pow(difference,2)
        distance = difference.sum(1) # take the sum of difference from all dimensions
        distance = distance ** 0.5
        sortdiffidx = distance.argsort()
    
    # find the k nearest neighbours
        vote = {} #create the dictionary
        for i in range(K):
            ith_label = labels[sortdiffidx[i]];
            vote[ith_label] = vote.get(ith_label,0)+1 #get(ith_label,0) : if dictionary 'vote' exist key 'ith_label', return vote[ith_label]; else return 0
        sortedvote = sorted(vote.iteritems(),key = lambda x:x[1], reverse = True)
        # 'key = lambda x: x[1]' can be substituted by operator.itemgetter(1)
        return sortedvote[0][0]

k = KNN() #create KNN object
group,labels = k.createDataset()
cls = k.KnnClassify([0,0],group,labels,3)
print cls

2. KNN应用于异常检测

KNN怎么进行无监督检测呢，其实也是很简单的，异常点是指远离大部分正常点的样本点，再直白点说，异常点一定是跟大部分的样本点都隔得很远。基于这个思想，我们只需要依次计算每个样本点与它最近的K个样本的平均距离，再利用计算的距离与阈值进行比较，如果大于阈值，则认为是异常点

通俗的算法描述：

KNN异常检测过程：对未知类别的数据集中的每个点依次执行以下操作

计算当前点与数据集中每个点的距离
按照距离递增次序排序
选取与当前点距离最小的k个点
计算当前点与K个邻居的距离，并取均值、或者中值、最大值三个中的一个作为异常值
根据预设阈值确定哪些为异常样本。

Yukai's Blog

KNN应用于异常检测

1. KNN

2. KNN应用于异常检测

3. Reference