1. Libra RCNN
paper: https://arxiv.org/pdf/1904.02701.pdf
“无痛涨点,实现简单,良心paper” 大概是对这篇论文最好的诠释了,作者来自浙大、港中文、商汤。

论文指出了通用检测方法中的三个层次的不平衡问题:
- sample level
- feature level
- objective level
这里引用作者知乎的一个解释:
这篇paper其实是对现有的detector training做了一个overall visit,现有大部分detector其实都遵从select region,extract feature,然后在multi-task loss的引导下逐渐收敛。那么,detector到底能不能train好,其实就跟这三部分关系很大。
- 选择的region够不够有代表性,能给training process提供更多的信息
- 抽取的feature能不能被后续的detector更好的利用
- 设计的objective function能不能引导整体训练更好的收敛
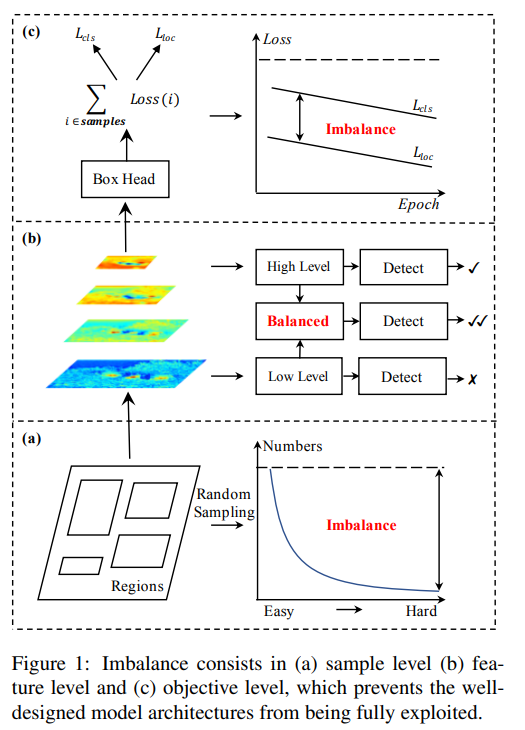
文章针对性的提出了解决这三种imblance问题的方法:
- 提出 IoU-balanced sampling 解决 sample level 的 imbalance
- 提出 balanced feature pyramid 解决 feature lavel 的 imbalance
- 提出 balanced L1 loss 解决 objective level 的 imbalance
2. 总体框架
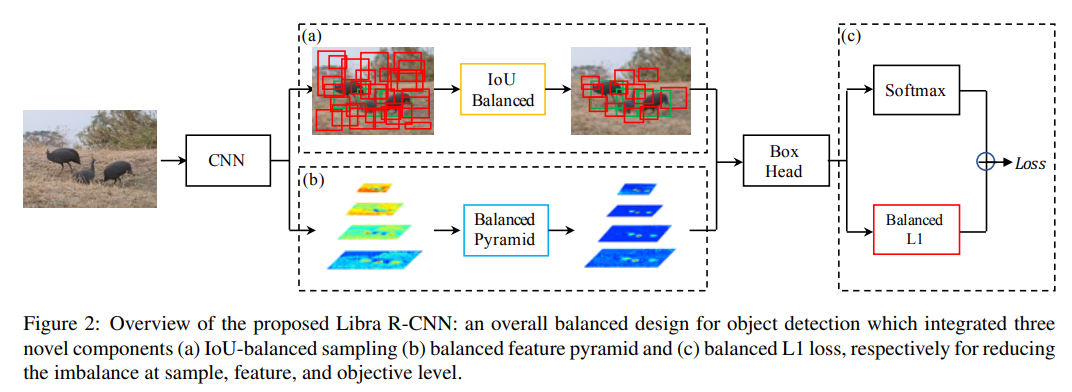
整个框架是非常典型的两阶段检测网络, 类似于Faster-RCNN,在RPN后采用了IoU Balanced的proposal采样策略。在共享特征图后增加了Balanced Pyramid的特征提取模块,在BoxHead中采用了提出的Balanced L1损失函数。
3. IoU balanced sampling
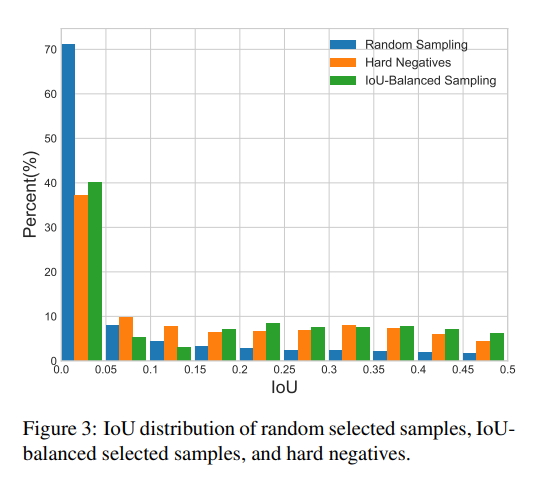
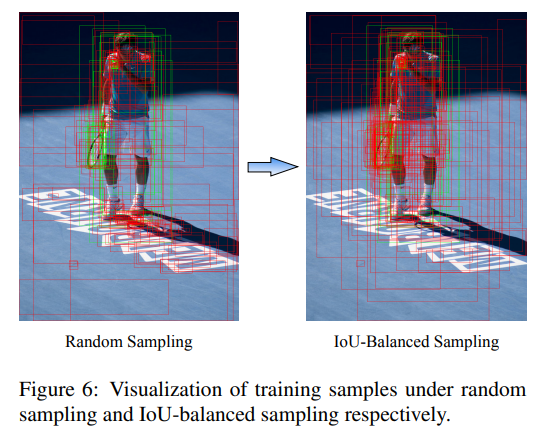
上图是三种采样策略在不同IoU下proposal分布,可以看到Hard Negative和 IoU-Balanced Sampling策略都可以较好的减少采样的样本在不同IoU下的imbalance。
随机采样到的样本超过70%都是在IoU在0到0.05之间的,这是因为觉得部分的proposal只包含背景区域,所以从统计学的角度考虑,随机采样很容易造成这种情况。OHEM可以有效的解决这个问题,但此方法容易受到 noisy label data的影响,且带来了额外的计算。
IoU balanced sampling 的做法如下,比较好理解
从 M 个负样本中,抽取 N 个负样本
对 IoU 值进行分箱操作,分成 k 个箱,实验中默认 k 为 3
从每个箱中随机抽取 N/k 个负样本
4. Balanced Feature Pyramid
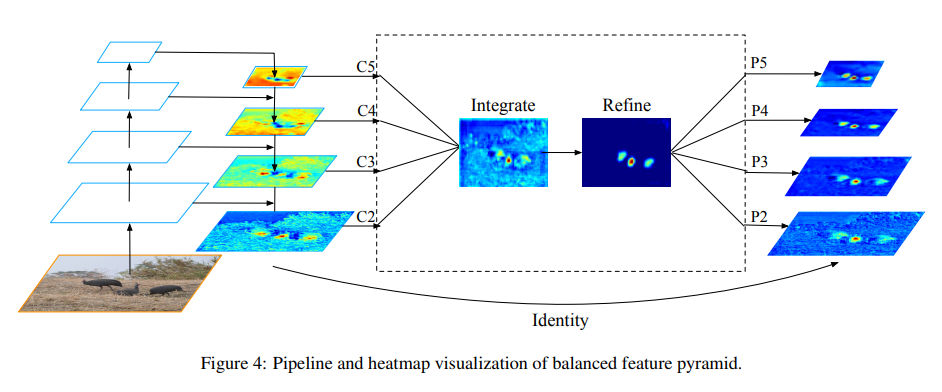
BFP模块包含四个步骤,rescale、integrate、refine、strength。
rescale and integrate,对FPN后的各层级特征图执行插值(interpolation)或者池化(max pooling)操作,统一为C4层级的特征图尺寸,然后对特征图进行加权取平均操作.
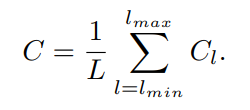
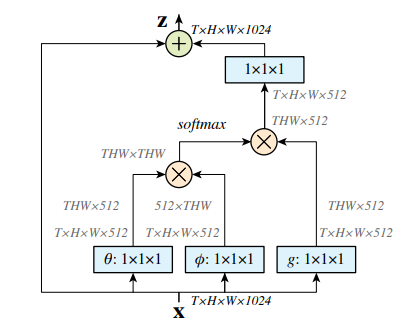
refine, 可以采用conv或者 non-local mldule(如下图)操作,论文中采用了 Gaussian non-local attention module, 可以enhance the integrated features。
strength, 将refine后的features进行插值得到P2,P3并与FPN后的C2、C3执行逐特征add操作,使用max pooling 得到P5,并于C5执行add, P4则直接与C4 add。
5. Balanced L1 Loss
引用作者的解释:
目标检测本质上还是一个多任务task,既要识别相应的类别,也要精准定位,那么他们两个在训练过程总的balance就比较tricky,但一味的提高regression的loss其实会让outlier的影响变大(类似于OHEM中的noise label)。于是我们通过特定的enhance比较重要部分的梯度来让这个过程更加smooth,在几个方面寻找一个相对balance的case。
这个地方,,说实话我没太看懂,能想出这种方法,数学功底不一般呀。
回顾一下Fast-RCNN的多任务损失函数,其由两部分组成,分类损失和BBox的回归损失,则用来平衡两个任务的损失。
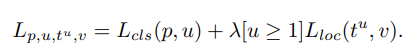
当样本损失大于等于1.0时的样本定义为outliers, 反之则为inliers, 若想直接通过调整权重增加回归损失的权重,会导致网络对outliers更加敏感,因为边界回归是无边界的。
再回顾一下Smooth L1 Loss:
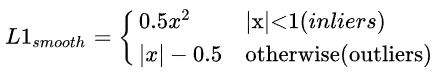
求导后:
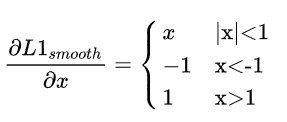
为了限制outliers的影响,将其损失值控制在1.0之内,并适当增大inliers的梯度值,Balanced Loss设计为
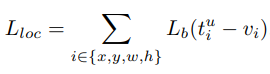
满足链式求导:
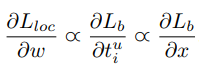
作者从需求出发,想要得到一个梯度当样本在 |x| < 1 附近产生稍微大点的梯度,作者设计了下面这个函数:
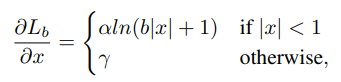
反推出损失函数Lb为:
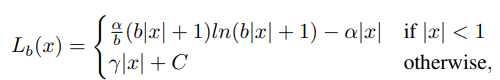
其中,
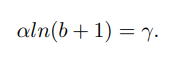
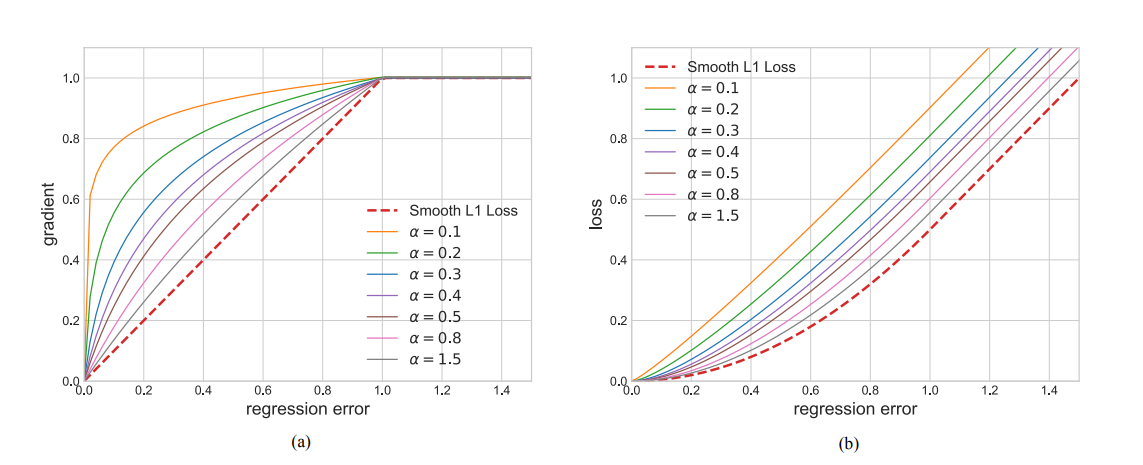
γ能够限制 outliers 的梯度大小。小的α能够提高 inliers 的梯度,并且对 outliers 的梯度没有影响,如上图所示。当回归损失值小于 1 时,balanced L1 Loss 中,小的α能够获得 (inliers 或者说是 easy samples) 更大的梯度;当损失值大于等于 1 时,(outliers 或者说是 hard sampling)梯度值保持不变。这种做法能够平衡 inliners 和 outliers,以达到更好平衡训练的目的。
实验中,默认为 α=0.5, γ=1.5。
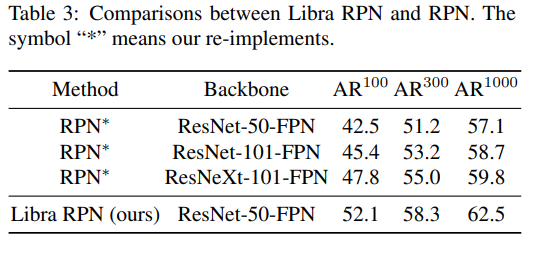
6. 实验效果