直方图均衡化

阅读原文

直方图均衡化，可以对在不同的光线条件下拍摄不同的图片进行均衡化处理，使得这些图片具有大致相同的光照条件。因此，我们可以用在训练模型之前，对图像进行对预处理。

直方图均衡

1. 直方图与对比度

首先，我们看下面的图像：

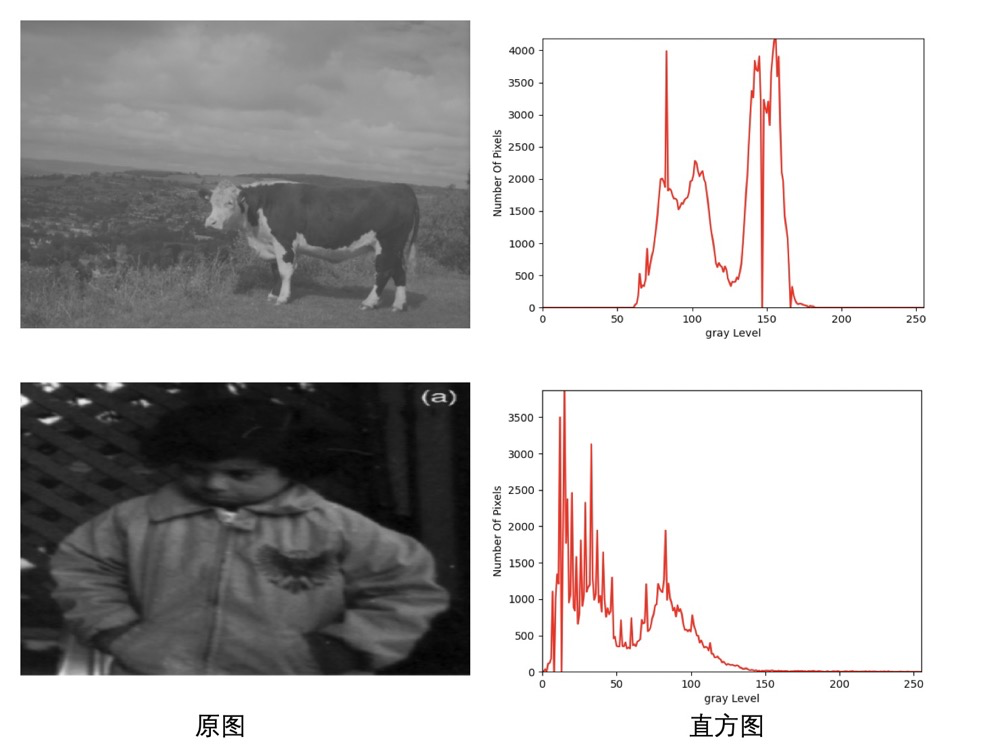
左列为原图，我们在观看的时候，感受很差。为什么很差呢？因为前景(关键区域)与背景太相似，无法很好的得到前景的信息。这就是表明，这些图像的对比度小，视觉体验很差。

其中，对比度是由两个相邻区域的亮度差异产生的。

对比度是使一个物体与其他物体区别开来的视觉特性上的差异。在视觉感知中，对比度是由物体与其他物体的颜色和亮度差异决定的，而我们的视觉系统对对比度比对绝对亮度更敏感。那么，如何量化一个图像中的对比度呢？我们先了解下直方图。

通过直方图我们可以看到各个灰度级的像素个数，即像素的分布情况。如果图像的大部分的像素都集中在直方图的某个范围，就表示图像中的大部分像素的灰度值差别很小，无法很好地进行分辨图像中的物体。

如原图像的像素值介于$5$~$10$之间（对比度是$10/5=2$）现将其映射到整个区域的输出图像到$0$ ~ $255$（对比度是$255/1=255$），由此可见，对比度得到了很大的提升。

2. 直方图的定义

图像的直方图：反应图像强度分布的总体概念。宽泛的来说直方图给出了图像对比度、亮度和强度分布信息。其中，强度就是一幅图像的像素取值，如$[0, 255]$。

其中，公式表示如下：

$h\left(r_{k}\right)=n_{k}$

其中，$n_{k}$是图像中灰度级为$r_{k}$的像素个数。 $r_{k}$是第$k$个灰度级，$k=0,1,2…L-1$。由于$r_{k}$的增量是$1$,直方图可以表示为$p(k)=n_{k}$。即，图像中不同灰度级像素出现的次数。

概括来说，直方图就是横坐标表示成像素值，纵坐标表示各个像素值的个数的图。

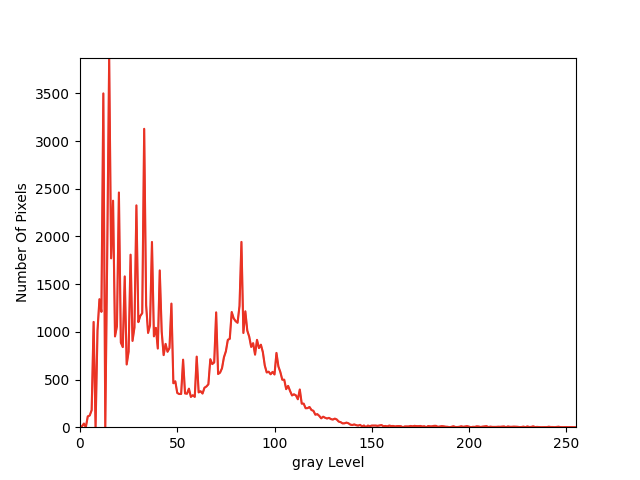
3.直方图均衡化的引入

若一幅图像的像素倾向于占据整个可能的灰度级并且分布均匀，则该图像有较高的对比度并且图像展示效果会相对好，于是便引出图像直方图均衡化，对图像会有很强的增强效果。

3.1 直方图归一化

先了解直方图归一化的概念，公式为：
$p(r_{k})=n_{k}/n$

$n$ 是图像的像素总数（如一幅$32*32$的图像，像素总数就是$1024$）。
$n_{k}$是图像中灰度级为$r_{k}$的像素个数
$r_{k}$是第$k$个灰度级，$k = 0,1,2,…,L-1$

因此，该函数主要有以下几个特性：

使函数值压缩到[0,1]区间。
给出灰度级$r_{k}$在图像中出现的概率密度统计。

3.2 直方图均衡化

直方图均衡化是建立在直方图归一化的基础之上。直方图均衡化的公式如下所示：

$s_{k}=\sum_{j=0}^{k}\frac{n_{j}}{n}, k=0, 1, 2,,,L-1$

注：

$n$是图像中像素的总和
$n_{j}$是当前灰度级的像素个数
$L$是图像中可能的灰度级总数

其中，直方图均衡化是采用的灰度级变换：$s = T(r)$，目的是欲将原始图的直方图变换为均匀分布的形式，这样就增加了像素灰度值的动态范围，从而达到增强图像整体对比度的效果。

代码如下：

import cv2
import numpy as np
import matplotlib.pyplot as plt

if __name__ == "__main__":
    # 读取图像并转换为灰度图
    img = cv2.imread(r'./imgs/boy.png')
    # 图像的灰度级范围是0~255
    # grayHist = cv2.calcHist([img], [0], None, [256], [0, 256])
    (b, g, r) = cv2.split(img)
    bH = cv2.equalizeHist(b)
    gH = cv2.equalizeHist(g)
    rH = cv2.equalizeHist(r)
    # 合并每一个通道
    result = cv2.merge((bH, gH, rH))
    res = np.hstack((img, result))
    cv2.imshow("dst", res)
    cv2.waitKey(0)

不能使用库函数，需要写出详细的直方图均衡化的过程：

import numpy as np


def hist_equalization(intput_signal):
    '''
    直方图均衡（适用于灰度图）
    :param intput_signal:   输入图像
    :return:    直方图均衡化后的输出图像
    '''

    output_signal = np.copy(intput_signal)   # 输出图像，初始化为输入

    intput_signal_cp = np.copy(intput_signal) # 输入图像的副本

    m, n = intput_signal_cp.shape # 输入图像的尺寸（行、列）

    pixel_total_num = m * n  # 输入图像的像素点总数

    p_r = []   # 输入图像的概率密度
    p_s = []   # 输出图像的概率密度

    # 求输入图像的概率密度函数
    for i in range(256):
        p_r.append(np.sum(intput_signal_cp == i) / pixel_total_num)

    # 求输出图像的概率密度函数
    single_pixel_class_probobility_t = 0  # 临时存储某一灰度级的概率
    for i in range(256):
        single_pixel_class_probobility_t = single_pixel_class_probobility_t + p_r[i]
        p_s.append(single_pixel_class_probobility_t)

    # 求解变换后的输出图像
    for i in range(256):
        output_signal[np.where(intput_signal_cp == i)] = 255 * p_s[i]

    return output_signal

其中关于像素的统计量如下：

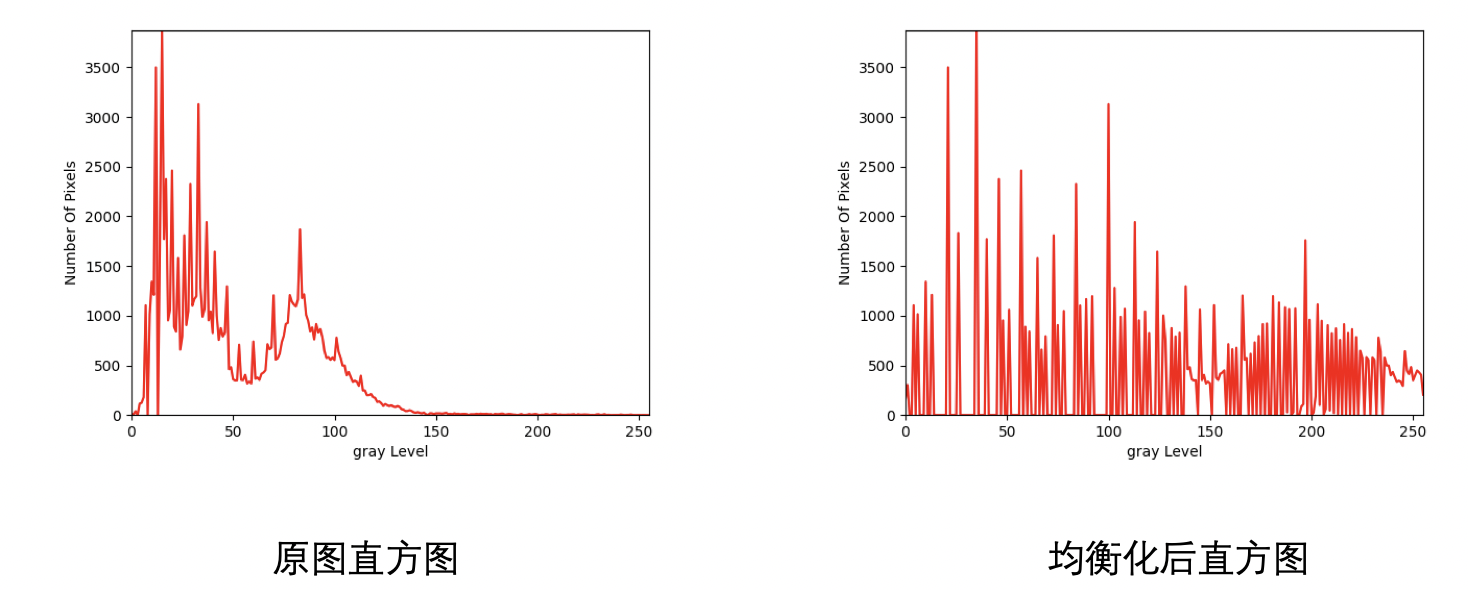
4. 小结

目前，基本的图像直方图均衡已经说完了，但是如果我们仔细看上图，会发现均衡化处理后对比度大大增强了，但是这个boy好像有点太亮了，这是因为这个直方图均衡化操作是对全局进行均衡化，直方图覆盖的范围太大，反而会丢失boy的一些信息。

因此，明天我们会继续沿着直方图均衡引入自适应直方图均衡化(AHE) 以及 限制对比度自适应直方图均衡化(CLAHE) 等直方图均衡化算法。

Yukai's Blog